Workshop on Multi-dimensional Proximity ProblemsJanuary 13, 2016, University of Maryland, College Park |
The workshop aims to bring together researchers in algorithms and data structures with an interest in multi-dimensional proximity problems (e.g. similarity search, approximate nearest neighbors, and more). It will feature a number of invited talks with emphasis on recent developments. We also provide possibility for participants to interact with the speakers and each other to discuss promising directions for future research. In particular, there will be the opportunity to bring and present a poster on work related to the theme of the workshop. The workshop is held the day after SODA '16, and the workshop location is easily reached from the SODA conference venue.
| 9.00-9.15 | Registration |
| 9.15-9.30 | Welcome David M. Mount, University of Maryland and Rasmus Pagh, IT University of Copenhagen |
| 9.30-10.15 | Scalable network distance browsing in spatial databases Hanan Samet, University of Maryland Abstract: An algorithm is presented for finding the k nearest neighbors in a spatial network in a best-first manner using network distance. The algorithm is based on precomputing the shortest paths between all possible vertices in the network and then making use of an encoding that takes advantage of the fact that the shortest paths from vertex u to all of the remaining vertices can be decomposed into subsets based on the first edges on the shortest paths to them from u. Thus, in the worst case, the amount of work depends on the number of objects that are examined and the number of links on the shortest paths to them from q, rather than depending on the number of vertices in the network. The amount of storage required to keep track of the subsets is reduced by taking advantage of their spatial coherence which is captured by the aid of a shortest path quadtree. In particular, experiments on a number of large road networks as well as a theoretical analysis have shown that the storage has been reduced from O(N^3) to O(N^1.5) (i.e., by an order of magnitude equal to the square root). The precomputation of the shortest paths along the network essentially decouples the process of computing shortest paths along the network from that of finding the neighbors, and thereby also decouples the domain S of the query objects and that of the objects from which the neighbors are drawn from the domain V of the vertices of the spatial network. This means that as long as the spatial network is unchanged, the algorithm and underlying representation of the shortest paths in the spatial network can be used with different sets of objects. Joint work with Jagan Sankaranarayanan and Houman Alborzi. Best Paper Award, SIGMOD Conference, Vancouver, June 2008. |
| 10.15-11.00 | Probabilistic Polynomials and Hamming Nearest Neighbors Josh Alman, Stanford University Abstract: We show how to compute any symmetric Boolean function on n variables over any field (as well as the integers) with a probabilistic polynomial of degree O(sqrt(n*log(1/eps)) and error at most eps. The degree dependence on n and eps is optimal, matching a lower bound of Razborov (1987) and Smolensky (1987) for the MAJORITY function. The proof is constructive: a low-degree polynomial can be efficiently sampled from the distribution. This polynomial construction is combined with other algebraic ideas to give the first subquadratic time algorithm for computing a (worst-case) batch of Hamming distances in superlogarithmic dimensions, exactly. To illustrate, let c(n):N->N. Suppose we are given a database D of n vectors in {0,1}^(c(n)*log n) and a collection of n query vectors Q in the same dimension. For all u∈Q, we wish to compute a v∈D with minimum Hamming distance from u. We solve this problem in n^(2−1/O(c(n)*log^2 c(n))) randomized time. Hence, the problem is in 'truly subquadratic' time for O(log n) dimensions, and in subquadratic time for d=o((log^2 n)/(loglog n)^2). |
| 11.00-11.30 | Break |
| 11.30-12.15 | Approximate Voronoi Diagrams: Techniques, tools, and applications to kth approximate nearest neighbor search Nirman Kumar, UC Santa Barbara Abstract: Approximate Voronoi Diagrams are a well known data structure for multidimensional approximate nearest neighbor search in Euclidean spaces when the dimension is low. They require linear space and logarithmic query time, thus extending the goodness of Voronoi diagrams in the plane, to higher dimensions. In this talk we will survey some of the techniques and theory behind them, and show how we can leverage those techniques to come up with a data structure for approximate kth nearest neighbor searching. |
| 12.15-13.45 | Lunch |
| 13.45-14.30 | Streaming Algorithms for Robust Distinct Elements Qin Zhang, Indiana University Bloomington Abstract: We study the problem of estimating distinct elements in the data stream model, which has a central role in traffic monitoring, query optimization, data mining and data integration. Different from all previous work, we study the problem in the *noisy* data setting, where two different looking items in the stream may reference the same entity (determined by a distance function and a threshold value), and the goal is to estimate the number of distinct *entities* in the stream. In this paper, we formalize the problem of robust distinct elements, and develop space and time-efficient streaming algorithms for datasets in the Euclidean space, using a novel technique we call bucket sampling. We also extend our algorithmic framework to other metric spaces by establishing a connection between bucket sampling and the theory of locality sensitive hashing. Moreover, we formally prove that our algorithms are still effective under small distinct elements ambiguity. Our experiments demonstrate the practicality of our algorithms. |
| 14.30-15.15 | Data-Dependent Hashing for Approximate Near Neighbors Alexandr Andoni, Columbia University Abstract: We show a new approach to the approximate near neighbor problem, which improves upon the classic Locality Sensitive Hashing (LSH) scheme. Our new algorithms obtain query time (roughly) quadratically better than the optimal LSH algorithms of [Indyk-Motwani'98] for the Hamming space, and [Andoni-Indyk'06] for the Euclidean space. For example, for the Hamming space, our algorithm has query time n^r and space n^{1+r}, where r=1/(2c-1)+o(1) for c-approximation. Our algorithms bypass the lower bounds for LSH from [O’Donnell-Wu-Zhou'11]. The new approach is based on hashing that itself depends on the given pointset. In particular, one of the main components is a procedure to decompose an arbitrary pointset into several subsets that are, in a certain sense, pseudo-random. Our data-dependent hashing scheme is optimal. Based on a few joint papers with Piotr Indyk, Huy Nguyen, and Ilya Razenshteyn. |
| 15.15-15.45 | Break and poster session |
| 15.45-16.30 | New Directions in Approximate Nearest Neighbors for the Angular Distance Thijs Laarhoven, TU Eindhoven Abstract: Given a large high-dimensional data set, the nearest neighbor problem asks to preprocess this data set in such a way that, given a target vector later, one can quickly find the vector in this data set closest to the target vector. Whereas finding an exact solution to this problem essentially requires a linear search through the data set, it is well known that finding an approximate solution can be done in sublinear time. A celebrated method achieving this sublinear query time complexity (and a subpolynomial preprocessing time complexity) is locality-sensitive hashing (LSH), and various LSH methods have been proposed in the last few decades for different metrics, and achieving different tradeoffs between practicality and asymptotic optimality. In this talk we will look at the approximate nearest neighbor problem for the angular distance (cosine distance), revisiting existing schemes from the literature, and seeing how different ideas can be combined to achieve even better results for large data sets, both in theory and in practice. We will first consider the "balanced" regime commonly considered in the literature, and then we will look at how we can obtain arbitrary tradeoffs between the preprocessing complexity and the query complexity, also improving upon related work in this area. |
| 16.30-16.45 | Closing |
 |
 |
 |
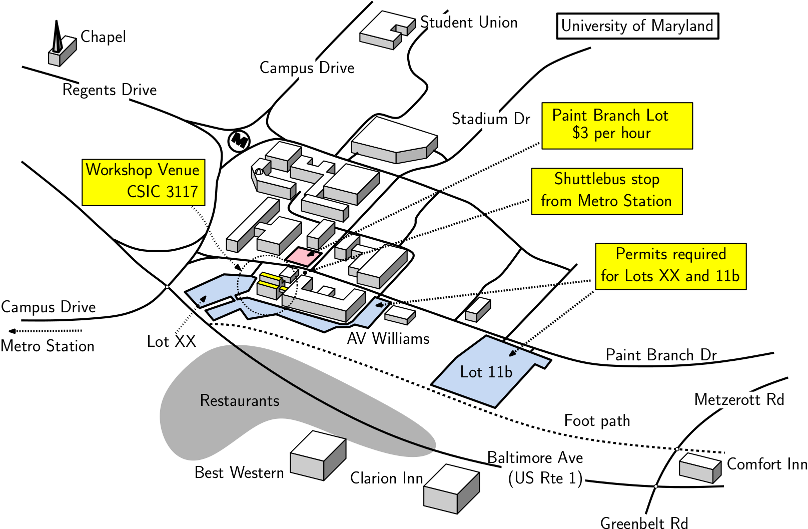
The Workshop will be held in CSIC 3117 on the third floor or the Computer Science Instructional Center (CSIC). This building is connected by a bridge to the A.V. Williams Building, where the Dept. of Computer Science is located (see the map below).
You can come from anywhere in the Washington DC area by the DC Metrorail system (System Map) and can get off at the College Park, University of Maryland Metro Station (on the Green Line). It is about a 20-minute walk to the campus, but you can take the free UM Shuttle Bus to the campus. (It is Bus 104. Here is the 104 Schedule.) Ask the driver to let you off at the first stop after entering the campus (in front of the Wind Tunnel Building). It is very close to the CSIC building (see the map below).
If you are staying at one of the closer hotels (e.g., Best Western, Clarion Inn, or Comfort Inn and Suites), and the weather is good, walking is the best way to get to campus. You can walk down Baltimore Avenue towards the main entrance on Campus Drive or the nice foot path that runs along the stream next to the campus. (You may need to ask someone to help find an access point.)
If you drive to campus, please note that parking is aggressively enforced. There are two options (see the map below).